Um die Natürlichen Vorgänge des Universums zu verstehen ist es nötig Messgrößen zu definieren. Diese Messgrößen werden in Physikalischen Einheiten gemessen, wobei unterschiedliche Einheitssysteme existieren. Diese Einheitssysteme ordnen einer Physikalischen Größe einen Wert zu. Um dieses Vorgehen zu verdeutlichen wird zunächst der Raum betrachtet.
I.1.1 Definitionen der Klassischen Mechanik
I.1.1.1 Raum und Zeit:
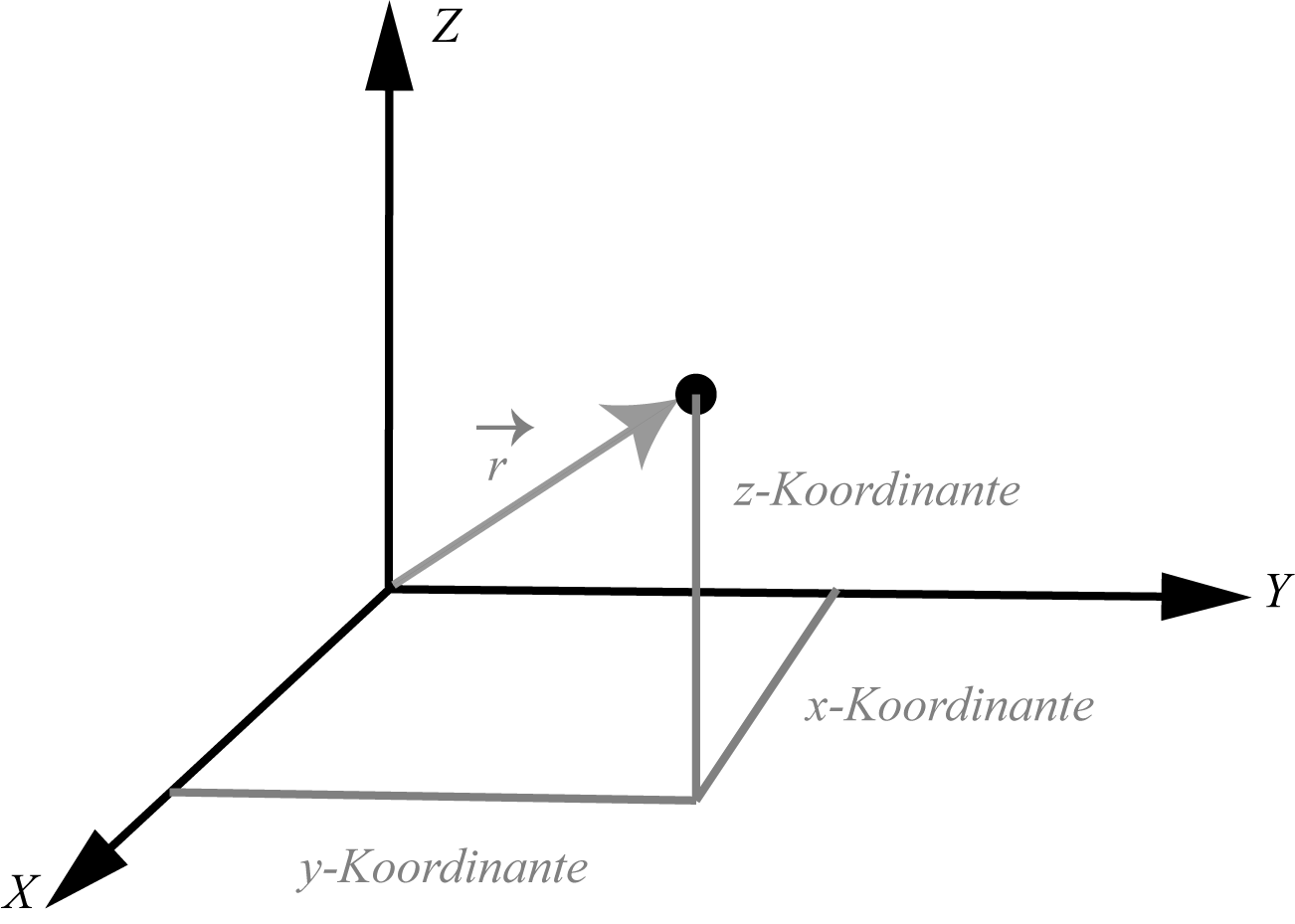
Im laufe der Geschichte wurde der Raum physikalisch des öfteren modifiziert. Jedoch ist der klassische Begriff des Raumes für die meisten alltäglichen Probleme ausreichend und wurde Jahrtausende lang mit Erfolg genutzt. Bereits die Griechen nutzten den Raum und ordneten ihm Punkte mit Zahlenwerten zu, den sogenannten Raumpunkten. Diese Punkte konnten nur mit Linien verbunden werden um die Richtung und die Länge der Abstände zu bestimmen. Mathematisch ist dies der Bereich der Vektorgeometrie. Dabei ist zu beachtet, dass wir in einer mindestenens dreidimensionalen Welt leben, jedoch Physikalische Probleme auf weniger Dimensionen approximiert werden können. Der Ortsvektor \(\vec{r}\) der vom Ursprung auf einen bestimmten Punkt im Raum zeigt ist dabei definiert als:
$$\vec{r} = x \vec{e_x} +y \vec{e_y} + z \vec{e_z}, \qquad (1.1)$$ Wobei \(x,y,z\) Streckungen von den Einheitsvektoren \(\vec{e_x},\vec{e_y},\vec{e_z}\) darstellen:
Abbildung 1.2: Kartessisches Koordinantensystem mit Ortsvektor der sich aus x,y,z Komponente zusammensetzt.
Es ist zu beachten, dass der Ort ein Punkt und somit ein Skalar, also einen Wert, darstellt. Wohingegen der Ortsvektor aus drei Koordinanten besteht und mathematisch in die Klasse der Vektoren mit allen Rechenregeln zugeordnet ist. Die Messwerte werden im SI (Système international d’unités) in Meter angegeben, jedoch ist zu beachten das nicht immer das Internationale Einheitsystem genutzt wird.
SI-Basiseinheiten 1: Das Meter [m]
Der Meter ist dadurch definiert, dass der Lichtgeschwindigkeit im Vakuum \(c\) ein fester Wert zugewiesen wurde und die Sekunde (s) ebenfalls über eine Naturkonstante, die Schwingungsfrequenz \(\Delta \nu_{Cs}\) definiert ist. $$c = 299.692.458 \frac{m}{s}.$$ $$1m = \frac{1}{299.792.458}\cdot c \cdot s.$$ Somit ist ein Meter definiert als die Länge der Strecke, die das Licht im Vakuum während der Dauer von 1/299.792.458 Sekunde zurücklegt. [2]
Nachdem der Raum ausführlich beschrieben wurde, widmen wir uns jetzt der Zeit \(t\). Die Zeit ist ein Mysteriöses Konstrukt, dass wir Menschen in Vergangenheit, Gegenwart und Zukunft zuordnen. Dieses Modell wird im laufe der Geschichte stark verzerrt, sodass Raum und Zeit später als Raumzeitkontinuum zusammengefasst werden und mit der Allgemeinen Relativitätstheorie die absolute Zeit verworfen wird. Dies wird in späteren Kapiteln ausführlicher behandelt. Zurzeit genügt es die Zeit als kontinuierlichen Pfeil zu betrachten der in eine Richtung, der Zukunft, verläuft. Die Einheit der Zeit ist im internationalen Einheitssystem die Sekunde. Wobei sie historisch nach der Erdrotation definiert wurde. Da die Rotationsbewegung der Erde jedoch mit Schwankungen hervorgeht wurde die Sekunde mittels technischer Entwicklung neu definiert:
SI-Basiseinheiten 2: Die Sekunde [s]
Die Sekunde ist das 9 192 631 770-fache der Periodendauer der Strahlung, die dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Grundzustandes von Atomen des Nuklids 133Cs entspricht. $$\Delta \nu_{Cs} = 9.192.631.770 Hz,$$ $$1s = \frac{9.192.631.770}{\Delta \nu_{Cs}}.$$ Definitionsgemäß ist die Sekunde also das Vielfache der Periode einer Mikrowelle, die mit einem ausgewählten Niveauübergang im Caesiumsatom in Resonanz ist. Daher wird sie als Atomsekunde bezeichnet. Atomuhren basieren auf der Messung dieses Übergangs. [2]
I.1.1.2 Die Masse:
Um zu den Newtonschen Axiomen fortzuschreiten benötigen wird noch eine Physikalische Größe, die Masse \(m\). Die Masse kann zunächst als Trägheit zur Bewegung angesehen werden. So ist aus dem Alltag bekannt, dass ein Würfel aus Gold eine andere Trägheit auf Bewegung ausübt als ein Würfel der selben Größe aus Styropor. In den folgenden Kapiteln wird der Raum mit der Masse verknüpft und es wird sich herausstellen, dass eine Krümmung des Raums Ursache für Masse ist und die Masse der Grund für die Krümmung der Raumzeit darstellt. Wie beim Raum und der Zeit benötigen wir in der klassischen Mechanik dieses Modell jedoch nicht um Problemstellungen elegant zu lösen und definieren die Masse auf grund ihr charakeristischen Trägheit.
SI-Basiseinheiten 3: Das Kilogramm [Kg]
Das Kilogramm ist die erste Einheit die ein veilfaches ihrer Ursprungseinheit darstellt. So ist ein Kilogramm das tausendfache eines Gramms. Grund hierfür ist, dass Ursprünglich ein Kilogramm die Masse von einem Liter Wasser entsprechen sollte, da dies für den Menschlichen Alltagsgebrauch am Sinnvollsten erschien. Jedoch stellte sich heraus, dass diese Definition nicht beständig war und auch ein Ur-Kilogramm, aus einer Legierung aus Platin und Iridium, keine konstante Masse vorweisen konnte. Zurzeit gibt es keine eindeutige Definition für das Kilogramm, jedoch werden zwei Experimentelle Aufbauten vorgeschlagen. Beide Experimente leiten die Masse aus der Plankschen konstante \(h\), die später ausfürhlich behandelt wird, ab. Das Eine Experiment trägt den Namen Watt-Waage und wird in Kanada prakteziert, das andere ist die XRCD-Methode (Avogadroprojekt), in Deutschland mit dem Versuch eine perfekte Silizium-Kugel herzustellen un ddie einzelnen Silizium-Atome abzuzählen. Dies würde auch zu einer genaueren Bestimmung der Avogadro-Konstante führen. [2]
Mit dem Wissen über des Meter und des Kilogramms, ist es nun auch möglich, einen Raum mit einer gewissen Masse zu definieren und diesen mit anderen Räumen zu vergleichen. Diese Größe wird als Dichte \(\rho\) bezeichnet und wird im laufenden eine wichtige Rolle einnehmen. $$ \rho = \frac{m}{V}, \qquad (1.2) $$ wobei \(V\) das Volumen also den Rauminhalt darstellt, dessen Einheit \(m^3\) ost und somit für die Dichte die Einheit \(\frac{kg}{m^3}\) erfolgt.
I.1.2 Die Newtonschen Axiome
In der beobachtbaren Natur besitzen Körper eine gewisse Ausdehnung im Raum. Diese Ausdehnung kann jedoch vernachlässigt werden, wenn wir uns immaginär vorstellen, dass die komplette Masse im Zentrum des Körpers konzentriert ist. Diese Körper nennen wir Punktmassen. Diese Vorstellung ist zwar unrealistisch, jedoch kann sie uns bei der Berechnung von komplizierten Gleichungen helfen und reicht in vielen Fällen, sogar bei der Planetenbewegung, vollkommen aus. Im folgenden wird jeder Körper als Punktmasse behandelt.
I.1.2.1 Die Beschleunigung:
Knapp 2000 Jahre nach Aristoteles Lehre der Bewegung, die Bewegung als etwas Göttliches ansah, stellte Galileo Galilei fest, dass die Zeit der Fallbewegung unabhängig von der Masse eines Körpers ist. Hierfür baute er ein Experiment auf, dessen Name heute als Galileis Fallrinne bekannt ist [Abbildung 1.4].
Hier wurden gleichgroße Kugeln ein schiefe Ebene heruntergerollt und mittels Einkerbungen auf der Ebene die zurückgelegten Strecken in gleichmässigen Zeitintervallen bestimmt. Die Kugeln besaßen jedoch unterschiedliche Dichten und müssten nach damaligen Verständnis unterschiedlich lang benötigen um die Ebene hinabzurollen. Galileo jedoch endeckte, dass die verstrichene Zeit bei jedem Körper gleich lang war. Zudem endeckte er, dass sich die Bewegung der Körper bei rollen veränderte. Sie beschleunigte sich zunehmend. Diese Änderung konnte erst Newton mittels der Intifisimalrechnung bestimmen, jedoch war es Galileos verdienst den Zusammenhang zwischen der Änderung der Geschwindigkeit und der Beschleunigung zu erkennen. Die Beschleunigung wird in der Physik mit dem Formelzeichen \(\vec{a}\) bezeichnet. Diese Vektorielle Größe ist die Änderung der Strecke pro Zeit oder in SI-Einheiten die Änderung eines (Meters pro Sekunde) pro Sekunde [\(\frac{m}{s^2}\)]. Auf der Erde und überall im Universum herrscht eine gewisse Beschleunigung, dessen Ursache wir später genauer betrachten. Auf der Erde ist diese sogannante Erdbeschleunigung \(\vec{g}\) näherungsweise überall gleich und beträgt: $$ \vec{g} = \left(\begin{array}{c} 0 \\ 0 \\ 9,81\end{array}\right) \frac{m}{s^2}. $$
Es ist zu ersehen, dass der Wert des Vektors lediglich in die z-Komponente zeigt und somit die Erdeschleunigung immer nach unten wirkt. Dies ist der Grund das Gegenstände fallen und es anstrengt sich mit einer Masse gegen diese Beschleunigung zu bewegen. Somit ist die Beschleunigung \(\vec{a}\) auf der Erde gleich \(\vec{g}\).
I.1.2.2 Die Geschwindigeit:
Ist die Bewegung jedoch konstant, also ist die zurückgelegte Strecke pro Zeitinterval immer gleich, wird physikalisch von der Geschwindigkeit \(\vec{v}\) gesprochen. Die Einheit dieser Größe ist dabei \(\frac{m}{s}\). Wir vorhin erwähnt, endeckte Newton die Mathematische Beziehung zwischen der Geschwindigkeit und der Beschleunigung mit folgender Gleichung: $$ \vec{v}= \int \vec{a} dt. $$
I.1.2.3 Trajoktorie:
Mit diesem Werkzeug war es nun Möglich die Trajoktorie also die Bewegung eines Körpers zu bestimmen. Hierbei wählte Newton folgende Notation: Die Trajoktorie also der Raumpunkt in abhängikeit der Zeit: \(\vec{r}(t)\) Die Geschwindkeit als Änderung der Trajoktorie pro Zeiteinheit: \(\vec{v}(t) = \dot{\vec{r}}(t) \) Die Beschleunigung als Änderung der Geschwindkeit pro Zeiteinheit: \(\vec{a}(t) = \dot{\vec{v}}(t) = \ddot{\vec{r}}(t) \) Wobei die Punkte für die zeitliche Ableitung der Größe stehen. Als Beispiel wird der freie Fall, also eine gleichmässig beschleunigte Bewegung bestimmt:
I.1.2.3.1 Freier Fall:
Da Beschleunigung der Erde kann als konstant angesehen werden somit ist \(\ddot{\vec{r}}= const. = \vec{-g} \). Mit der Definition der Geschwindkeit ergibt sich: $$ \dot{\vec{r}} = \int \ddot{\vec{r}} dt = \int \left(\begin{array}{c} 0 \\ 0 \\ -g\end{array}\right) dt $$ $$ \rightarrow \dot{\vec{r}} = \left(\begin{array}{c} v_{0,x} \\ v_{0,y} \\ -g \cdot t + v_{0,z}\end{array}\right), $$ Hierbei steht die Integrationskonstante \(vec{v}_0\) für die Anfangsgeschwindigkeiten des Körpers. Beim freien Fall sind diese Komponenten 0 und fallen für die weitere Rechnung weg, jedoch werden sie für den Allgemeinen Fall stehen gelassen. Die Trajoktorie wird mit einer weiteren Integration bestimmt: $$ \vec{r} = \int \dot{\vec{r}} dt = \int \left(\begin{array}{c} v_{0,x} \\ v_{0,y} \\ -g \cdot t + v_{0,z}\end{array}\right) dt $$ $$ \rightarrow \vec{r} = \left(\begin{array}{c} v_{0,x} \cdot t + r_{0,x} \\ v_{0,y} \cdot t + r_{0,y} \\ \frac{-g}{2} \cdot t^2 + v_{0,z} \cdot t + r_{0,z} \end{array}\right), $$ Dies kann Elegant in Vektorieller Form geschrieben werden: $$ \vec{r}(t) = \vec{r}_0 + \vec{v}_0 \cdot t + \frac{\vec{a}}{2} \cdot t^2 \qquad (1.3) $$ Beim freien Fall wird von einer gewissen Höhe \(z_0\), mit einer Geschwindigkeit \(\vec{v}_0 = 0\) ein Körper fallen gelassen. Somit sind die \(x\)- und \(y\)- Komponente zu vernachlässigen und wir erhalten: $$ \vec{r}(t) = z_0 - \frac{g}{2}t^2. $$ Wird als Zielpunkt der Boden gewählt also \(\vec{r}=0\) und die Gleichung nach t umgestellt ergibt sich die Fallzeit: $$ t = \sqrt{\frac{z_0}{g/2}} = \sqrt{\frac{2 z_0}{g}}. $$
I.1.2.3.2 Schräger Wurf:
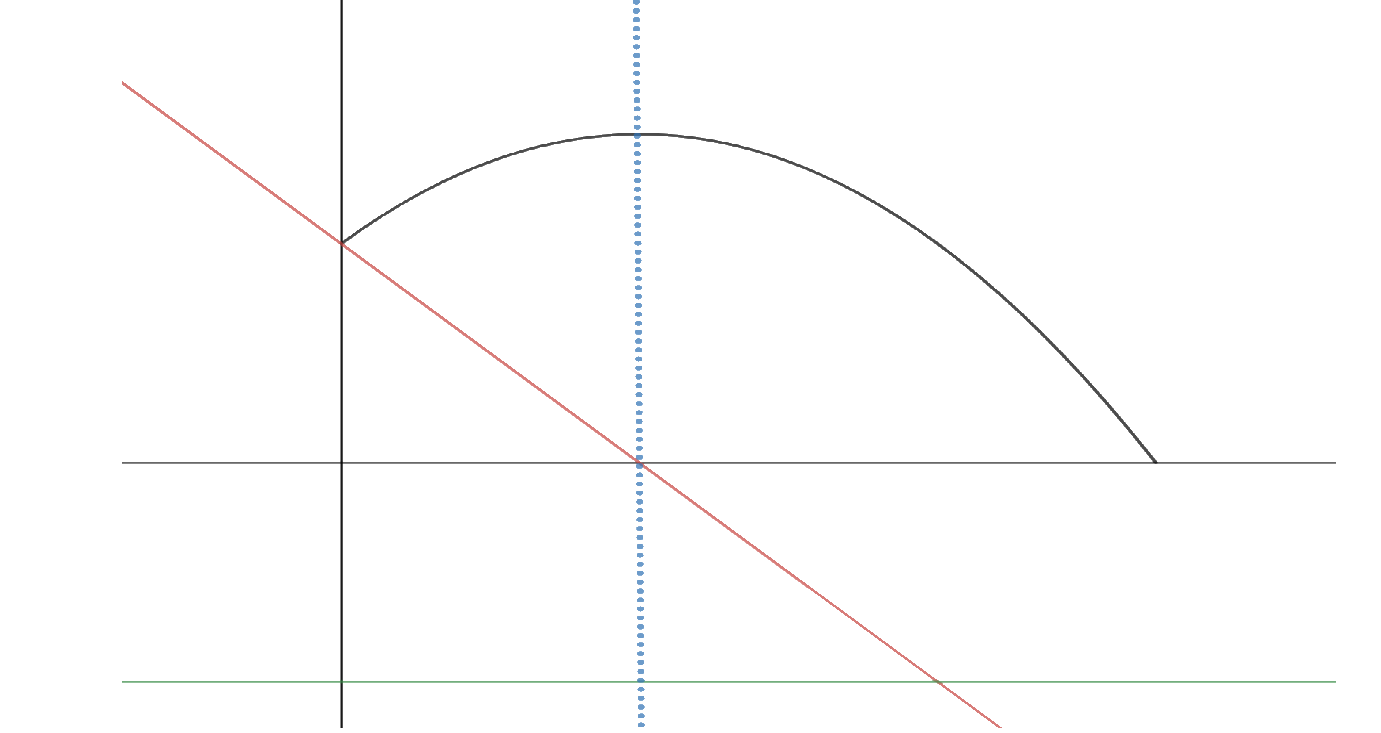
Eine andere Situation entsteht wenn eine Anfangshöhe \(z_0\) und eine Anfangsgeschwindkeit \(\vec{v}_0\) vorhanden sind. In diesem Fall (1.3) wird die Form eine Parabel annehmen:
Dabei ist deutlich der Zusammenhang zwischen Beschleunigung, Geschwindigkeit und Ort zu ersehen, so hängt die Wurfhöhe von der Abwurfhöhe, der Geschwindigkeitskomponente in z-Richtung und der Erdbeschleunigung ab. Wird der Betrag der Geschwindkeit genommen ergibt sich aus Gleichung (1.3) für die z-Komponente: $$ z(t)= z_0 + v_0 \sin(\vartheta) \cdot t - \frac{g\cdot t^2}{2}. $$ Um die maximale Höhe zu bestimmen, können wir wie aus der Kurvendiskussion bekannt die Ableitung der Funktion bildet und diese 0 setzten. $$ \dot{z}(t)=0=v_0 \sin(\vartheta)-g\cdot t, $$ Da die Zeit unbekannt ist wird die Formel nach \(t\) umgestellt, so erhalten wir den Zeitpunkt, andem die maximale Wurfhöhe erreicht wird. $$ \rightarrow \qquad t(z_{max})= \frac{v_0\sin(\vartheta)}{g}. $$ Hierbei ist wichtig, dass die x-Achse die Zeit darstellt. Nachdem die Zeit bekannt ist kann diese in Gleichung (1.3) eingesetzt werden um die Höhe zu bestimmen.
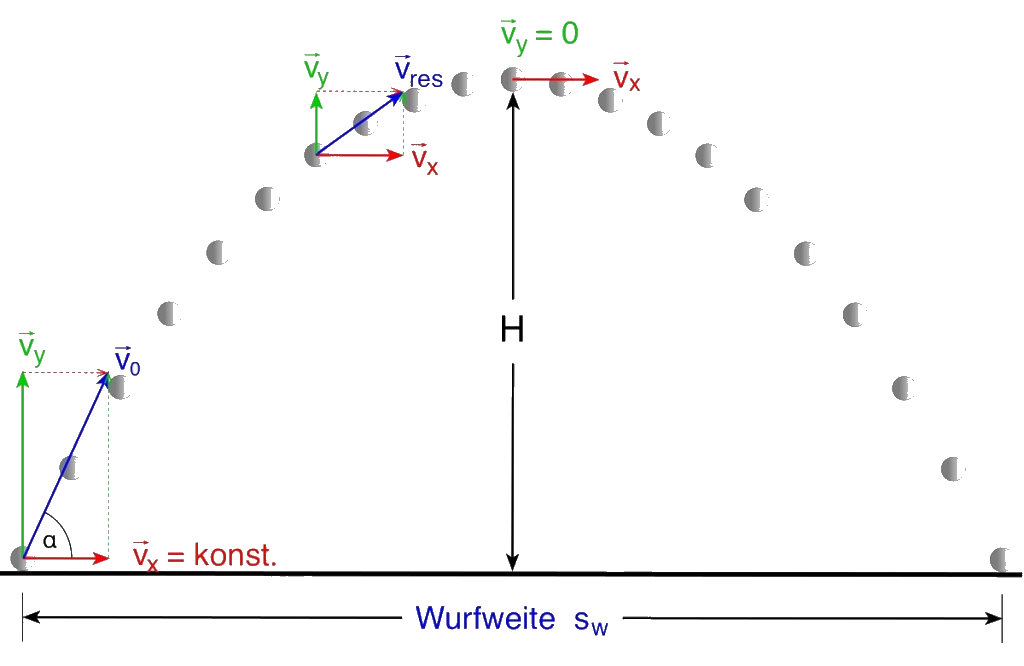
Abbildung 1.3:
Der schräge Wurf ist jedoch um einiges komplexer, dies wird jedoch später Behandelt, wenn wir Reibung berachten.
I.1.2.4 Newtonsche Axiom:
Die Newtonschen Axiome wurden 1686 von Sir Isaac Newton in seinem Werk Philosophiae Naturalis Principia Mathematica aufgestellt und vereinten die Forschungsergebnisse von Galileo Galilei und Keplers zu einer einheitlichen Theorie der Gravitation. Für Newton war der Raum sowie die Zeit absolut und führten ihm zu Erkenntnis, dass die Welt eine deterministische sei und somit Vergangenheit und Zukunft bereits vorherbestimmt sind. Diese Meinung werden wir im späteren Kapitel der Quantenmechanik verwerfen müssen, jedoch nehmen wir bisdahin an das unsere Welt einem Uhrwerk gleicht und jede Bewegung vorhersagbar ist. Historisch soll Newton die Gesetzt der Gravitation und das mathematische Werkzeug der Intifisimalrechnung bereits entdeckt haben, als er sich als Kind 1665 vor der Pest in seinem Elternhaus versteckte.
I.1.2.4.1 Erstes Newtonsches Axiom:
Aus den gewonnen Erkenntnissen kann nun das 1. Newtonsche Axiom hergeleitet werden. Dieses Gesetz wird als Trägheitsprinzip bezeichnet und besitzt folgende Formulierung:
"Jeder Körper beharrt in seinem Zustand der Ruhe oder der gleichförmigen Bewegung, wenn er nicht durch einwirkende Kräfte gezwungen wird, seinen Zustand zu ändern."
Diese Formulierung definiert Mathematisch den Impuls eines Körpers: $$ \vec{p} = m \cdot \dot{\vec{r}}. \qquad (1.4) $$
I.1.2.4.2 Zweites Newtonsches Axiom:
Das 2. Gesetz wird als Aktionsprinzip bezeichnet und definiert die Kraft mit folgendem Wortlaut:
"Wirkt auf einen Körper eine Kraft, so wird er in Richtung der Kraft beschleunigt. Die Beschleunigung ist der Kraft direkt, der Masse des Körpers umgekehrt proportional."
Mathematisch sieht die Formulierung folgendermassen aus: $$ \vec{F} = m \cdot \ddot{\vec{r}}. \qquad (1.5) $$ Die Kraft ist somit nichts anderes als die zeitliche Änderung des Impulses: $$ \vec{F} = \frac{d\vec{p}}{dt}. \qquad (1.6) $$
I.1.2.4.3 Drittes Newtonsches Axiom:
Das 3. Newtonsche Gesetz wird als Reaktionsprinzip bezeichnet und stellt eine Reaktionsbeziehung zwischen der Kraft und ihrer Gegenkraft dar. Ihre Formulierung lautet
"Besteht zwischen zwei Körpern A und B eine Kraftwirkung, so ist die Kraft, welche von A auf B ausgeübt wird, der Kraft , die B auf A ausübt entgegengesetzt gleich."
Mathematisch kann dies folgendermassen geschrieben werden: $$ \vec{F}_{A-B} = -\vec{F}_{B-A}. \qquad (1.7) $$ Dies kann kurz mit dem Ausdruck "actio gleich reactio" beschrieben werden.
I.1.2.4.4 Viertes Newtonsches Axiom:
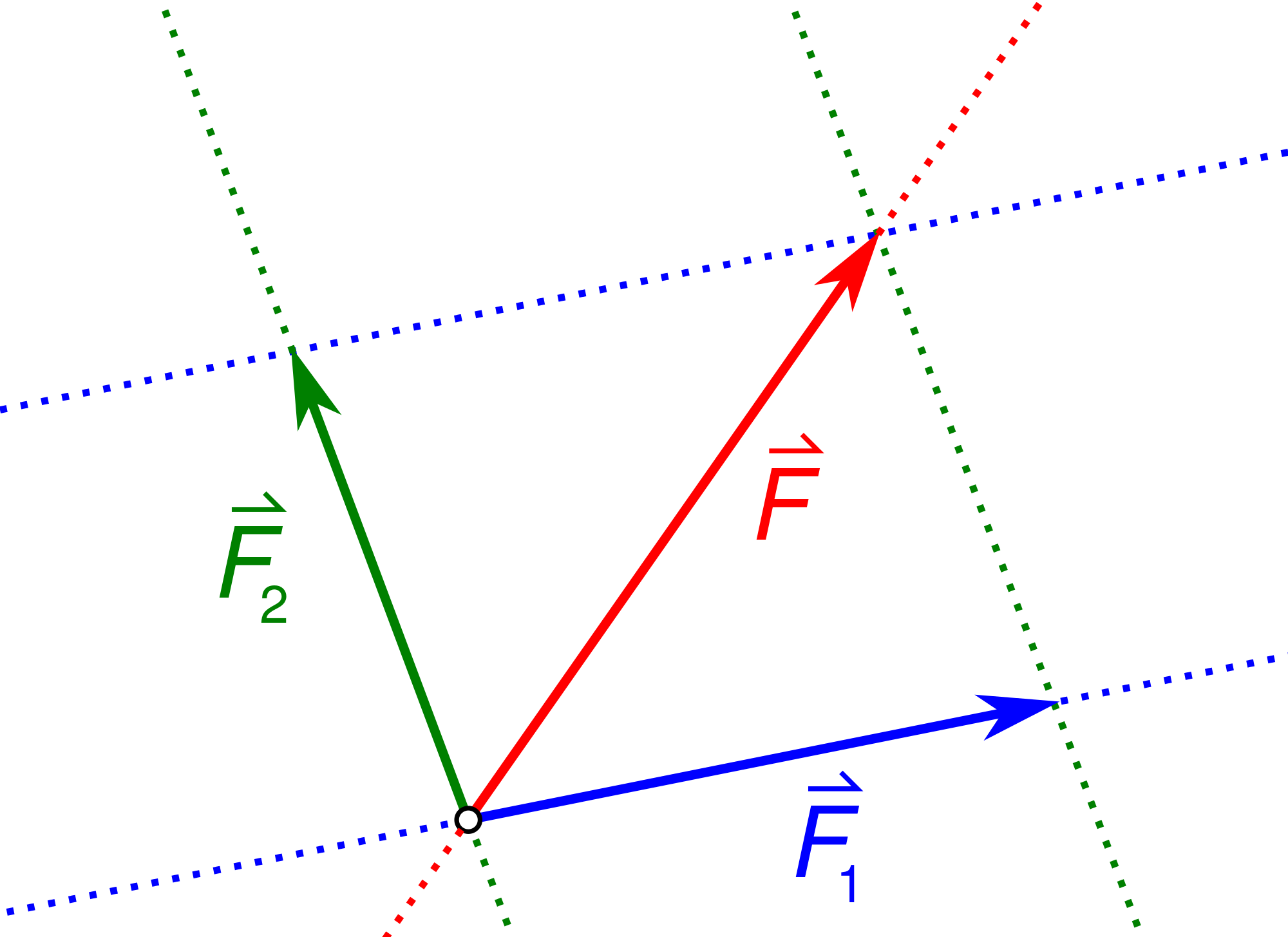
Das Vierte Newtonsche Gesetz ist eine Erweiterung der drei Axiome und wird als Superpositionsprinzip bezeichnet. Hierbei gelten die Gesetzte der Vektoraddition, somit addieren sich mehrere Kräfte zu einer resultierenden Kraft. $$ \vec{F} = \sum_i \vec{F}_i. \qquad (1.8) $$
Folgendes Illustration soll das Superpositionprinzip verdeutlichen:
I.1.2.5 Dissipative Kräfte:
Wie im 3. Newtonschen Axiom bereits erwähnt führt jede Kraft auf einem Körper auf eine entsprechende Gegenkraft. Das Populärste Beispiel hierfür ist der Legendere Apfel von Newton. Dieser hing am Baum und die Masse der Erde zog an ihm. Jedoch wurde der Apfel mit einer gleichgroßen entgegengesetzten Kraft vom Ast des Baumes gehalten. Dieses Kräftegleichgewicht hielt solange, bis sich Sir Isaac Newton nicht unter dem Baum saß, in diesem Moment hatte der Ast nichtmehr genug Kraft und die Anziehung der Erde gewann. Nicht zuvergessen sei jedoch, dass der Apfel auch die Erde anzog, jedoch seine Masse im vergleich zur Erde so gering war, dass die Bewegungsänderung der Erde vernachlässigbar ist. Die Legende über "Newton und dem Apfel der Erkenntnis" ist jedoch ein Ammenmärchen, welches doch praktisch für die ein oder andere Erklärung ist.
I.1.2.5.1 Die geneigte Ebene:
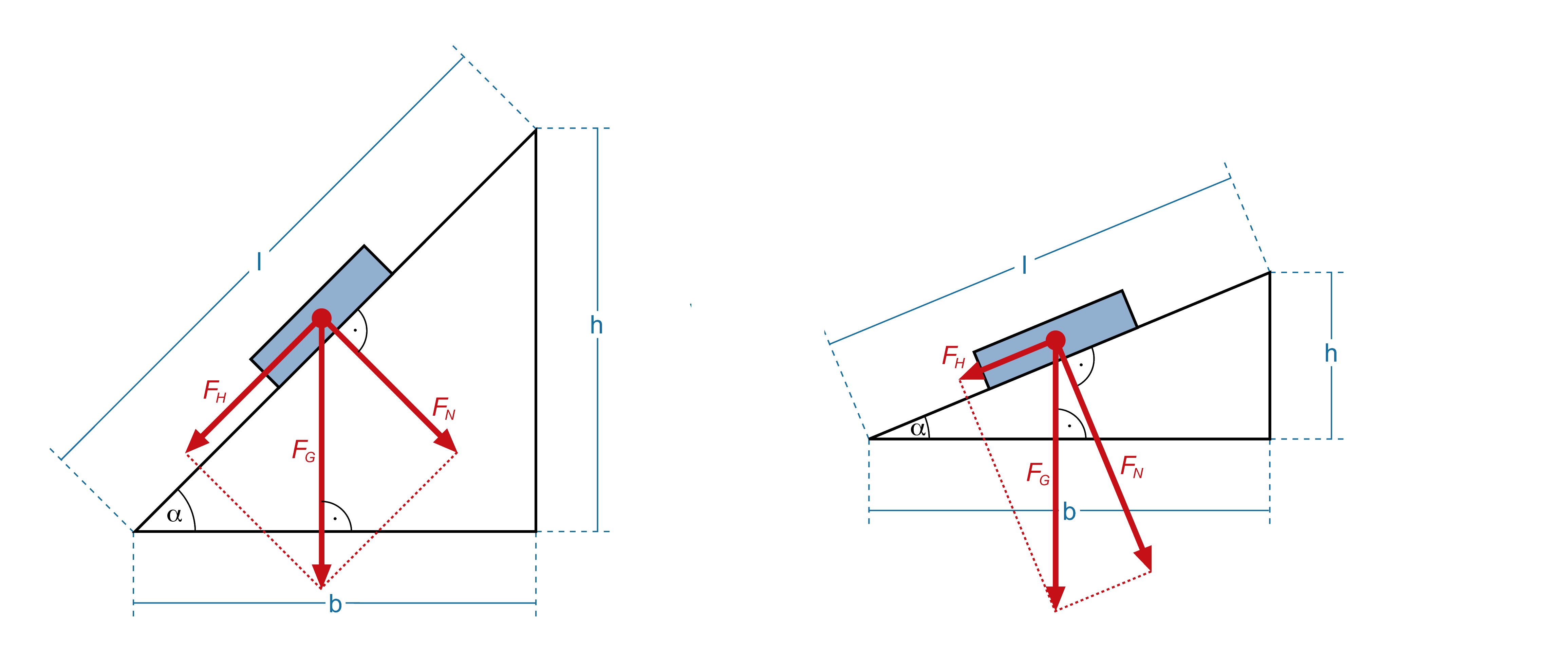
Die geneigte Ebene ist eine Fallbeispiel, dass uns das Reaktionsprinzip am deutlichsten veranschaulicht. So ist ein Körper der sich auf einer geraden ebene befindet im Kräftegleichgewicht. Einerseits zieht die Erdgravitation an den Körper, andererseits entsteht eine sogannante Normalkraft in Entgegengesetzter Richtung. Diese Normalkraft entsteht Hauptsächlich durch die Abstoßung einzelner Atome an den Grenzflächen der Körper, diese Kräfte werden später Kapiteln genauer Betrachtet. Wird die Ebene um ein Winkel \(\vartheta\) verschoben, spalten sich die Kräfte der der Gravitationswelchselwirkung in ihre horizontale und vertikale Richtung auf. Dabei ist es zunächst irrelevant welche Form der Körper besitzt, die Kräfte wirken auf eine Kugel ebenso stark wie auf einem Quader [Abbildung 1.6],
Jedoch geschieht in der Praxis ein deutlicher Unterschied, so rollt eine Kugel bereits bei einem viel kleineren Neigungswinkel die Ebene hinunter, als ein Quader. Außerdem steuern auch die Oberflächeneigenschaften der Materialien ebenso die Bewegung mit. Sind die Newtonschen Gesetzte Falsch? Die ernüchternde Antwort ist nein, denn die Natur ist voll mit Teilchen die Kräfte und Impulse weiterleiten. So herrscht bei unsere geneigten Ebene ein gewisser Luftwiderstand und dieser ist bei dem Quader größer als bei einer Kugel. Außerdem entsteht Reibung an den Kontaktflächen zwischen Ebene und Körper und auch diese sind beim Quader größer als bei seinem Gegenstück. Bereits so ein kleines System kann komplexe Berechnungen verlangen. Deshalb betrachten wir zunächst das System ohne Reibung.
a) Reibungsfreie geneigte Ebene:
Wie in Abbildung 1.6 zu ersehen kann die Kraft \(\vec{F}_G\) die auf dem Körper wirkt mit dem Pythagoräischen Lehrsatz in seine Komponenten \(\vec{F}_H\) und \(\vec{F}_N\) zerlegt werden. Wobei die Komponente von \(\vec{F}_H\) als Hangantriebskraft bezeichnet wird und parallel zur Schiefen Ebene liegt. Dieser Kraftanteil ist verantwortlich für Bewegung des Körpers und steigt bei vergrößerten Winkel, bis er bei 90° maximal wird und genau der Gravitationskraft \(\vec{F}_G\) entspricht. Durch Kräftezerlegung erhalten wir: $$ \vec{F}_G = \vec{F}_H + \vec{F}_N $$ Da die Gravitationskraft in z-Richtung wirkt und die Hypertensuse bei der Kräfteaddition darstellt, kann die Hangabtriebskraft als Ankatete und die Normalkraft als Gegenkatete betrachtet werden. Der Winkel \(\vartheta\) kann bestimmt werden indem wir \(\vartheta = 180°-90°-\alpha\) berechnen. Mit den Trigonometrischen Identitäten für ein Rechtwinkliges Dreieck ergibt sich für die Beträge der Kräfte: $$ F_H = sin(\vartheta) \cdot F_G, $$ $$ F_N = cos(\vartheta) \cdot F_G. $$ Aus dem Aktionsprinzip (1.5) ist bekannt, dass diese beiden Gleichung folgendermassen umgeschrieben werden können: $$ \vec{F}_H = m \cdot sin(\vartheta) \cdot \vec{a}, $$ $$ \vec{F}_N = m \cdot sin(\vartheta) \cdot \vec{a}. $$ die Ausdrücke können zusammengefasst werden als: \(\vec{a}_N\) und \(\vec{a}_H\) und umgestellt werden: $$ \vec{a}_H = \frac{\vec{F}_H}{m}, $$ $$ \vec{a}_N = \frac{\vec{F}_N}{m}. $$ Da wir nur die Hangabtriebskraft für die Bewegung benötigen können wir (1.3) verwendet. Mit einer Anfangshöhe \vec{r_0} und einer Anfangsgeschwindigkeit \(v_0=0\) ergibt sich für die Bewegung: $$ \vec{r}(t) = \vec{r}_0 - \frac{\vec{a}_H}{2}\cdot t^2$$ Mit den Trigonometrischen Zusammenhänge ergibt sich für die \(x\)- und \(z\)- Komponente folgende Gleichungen: $$ x(t) = x_0 \cos(\vartheta) -\frac{g}{2}\cdot \sin^2(\vartheta) \cdot t^2, $$ $$ y(t) = x_0 \sin(\vartheta) -\frac{g}{2}\cdot \sin(\vartheta)\cos(\vartheta) \cdot t^2. $$ Bei den am Anfang genannten Extremfällen ergeben sich folgende Gleichungen: $$ \vartheta= \frac{\pi}{2}=90° \qquad \rightarrow \qquad x(t)=0,\qquad y(t)=y_0-\frac{g}{2}t^2, $$ $$ \vartheta=0 \qquad \rightarrow \qquad x(t)=x_0, \qquad y(t)=0. $$ Wobei der erste Fall den freien Fall entspricht und der zweite Fall ein Ruhesystem darstellt.
b) Geneigte Ebene mit Reibung:
I.1.3 Koordinatensysteme und Transformationen
Koordinantesysteme bilden ein Zentrales Themengebiet für die Lösung jedes Physikalischen Prozesses. So kann es Vorteile bringen, wenn unterschiedlichen Koordinatensysteme genutzt werden. Das wohl berühmteste System ist das Kartesische Koordinatensystem nach René Descartes. Dieses System kommt uns am natürlichsten vor, da die einzelnen Einheitsvektoren Orthogonal aufeineinander stehen und somit jede Richtung linear unabhängig ist.
Die Wahl der Koordinanten solte jedoch invariant gegenüber unser Physikalischen Gesetzen sein. So sollte es keinen unterschied der Bewegungen eines Teilchens geben, ob wir das Koordinantensystem am Rand oder im Zentrum eines Hurrikans legen. Jedoch kann die Wahl uns die Rechnungen erleichtert, da unerwünschte Effekte bei adäquater Wahl wegfallen.
I.1.3.1 Die Galileo Transformation:
Galileo Galilei stellte bei seinen Arbeiten zur Bewegung von Körpern fest, dass eine einfache Transformation existiert um die Bewegung in unterschiedlichen Koordinantensystem zu beschreiben. Hierbei ist die Vorraussetzung, dass es sich beide Koordinatensysteme um gleichförmig geradlinige (später auch Drehung/Veschiebung) Bewegung unterscheiden. Als Beispiel nehmen wir das Zentrum eines Hurrikans: Im Zentrum befindet sich Alice \(A\), von außen betrachtet Bob \(B\) die Bewegung von Alice. Wir nehmen an, dass der Hurrikan auf magische Weise Alice mitbewegt, sich jedoch Alice dabei nicht vom Zentrum des Hurrkans wegbewegt. In diesem Fall ist das Koordinantensystem \(K\) von Alice in Ruhe, ihr Nullpunkt befindet sich im Zentrum des Hurrikans und da sie die Außenwelt vom Zentrum der Sturmes nicht wahrnehmen kann hat sie den Eindruck in Ruhe zu behaaren. Bob jedoch nimmt wahr, dass sich der Hurrikan mit einer konstanten Geschwindigkeit \(\dot{\vec{r}}\) fortbewegt und somit verschiebt sich in seinem Koordinatensystem \(K'\), das Zentrum des Sturms. Es scheint ein Paradox zu geben, denn obwohl sich Alice bewegt mit dem Sturm bewegt, scheint es für sie vollkommen Ruhig. Doch beide Perspektiven bestätigen das selbe Phänomen. Newtons Trägheitsprinzip (I. Gesetz) gibt uns hier die Antwort. Es handelt sich um ein sogenanntes Inertialsystem, Alice Geschwindigkeit ist konstant und somit kann ihre Bewegung, je nach Wahl des Koordinantensystems, als Ruhebewegung betrachtet werden. Verdeutlichen können wir es uns im kosmischen Maßstab: So scheint es Ihnen als Leser, dass sie gerade in vollkommender Ruhe verhaaren. Jedoch sind Sie eventuell in einem Auto oder in einem Zug und ihr Gefährt befindet sich auf der Erde, die mit unglaublichen 108.000 \(\frac{km}{h}\) um die Sonne ihre Bahnen dreht. Dies ist jedoch noch nicht alles die Sonne wiederum bewegt sich mit knapp 900.000 (\frac{km}{h}\) um das Zentrum der Milchstraße und die Milchstraße wiederrum bewegt sich auf unsere Nachbargalaxie Andromeda zu. Diese beiden Galaxien und einige anderen Zusammen bilden den Virgo-Galaxienhaufen und diese gehören einer noch größeren Struktur dem sogannten Supergalaxienhaufen Laniakea an. Eine unglaubliche Dynamik jedoch scheint es Ihnen als Leser, dass Sie in Ruhe verhaaren. Das Wesen des Inertialsystems werden wir besonders im Bereich der Relativitätstheorie noch genauer betrachten und werden eine andere Seite der Zeit entdecken die unserem alltäglichen Anschauungen komplett widerspricht. Doch wie können wir jetzt die Koordinantensysteme von Alice und Bob in Einklang bringen? Die Antwort ist ganz einfach wir fügen die Differenzgeschwindigkeit \(v\) beider Systeme hinzu:
Galileo Transformation:
$$ \left(\begin{array}{c} x' \\ y' \\ z' \\ t' \end{array}\right) = \left(\begin{array}{c} x-v\cdot t \\ y \\ z \\ t \end{array}\right) , \qquad (1.9a) $$ In diesem Beispiel würde sich der Hurrikan entlang der x-Richtung bewegen. Würden wir beispielsweise eine Geschwindigkeit in x-Richtung von 150 km/h annehmen und zwei Stunden beobachten so wäre die x-Position von \(A\) bei \(x=300km\), da sich die Koordinantensysteme von Alice und Bob genau mit dieser Geschwindigkeit auseinander bewegen würden wir nach einsetzen in der Formel für \(x'=0\) erhalten. Und somit wären beide Koordinantensysteme im Einklang miteinander. Selbstverständlich kann diese Transformation auch in die andere Richtung durchgeführt werden wobei sich das Vorzeichen von \(v\) ändert:
Inverse Galileo Transformation:
$$ \left(\begin{array}{c} x \\ y \\ z \\ t \end{array}\right) = \left(\begin{array}{c} x' + v\cdot t \\ y' \\ z' \\ t' \end{array}\right) . \qquad (1.9b)$$ Natürlich kann die Zeit auf die selbeweise transformiert werden, so wird einfach die Differenz der Uhrzeiten \(\Delta t\) addiert bzw. subtrahiert.
I.1.3.2 Polarkoordinaten:
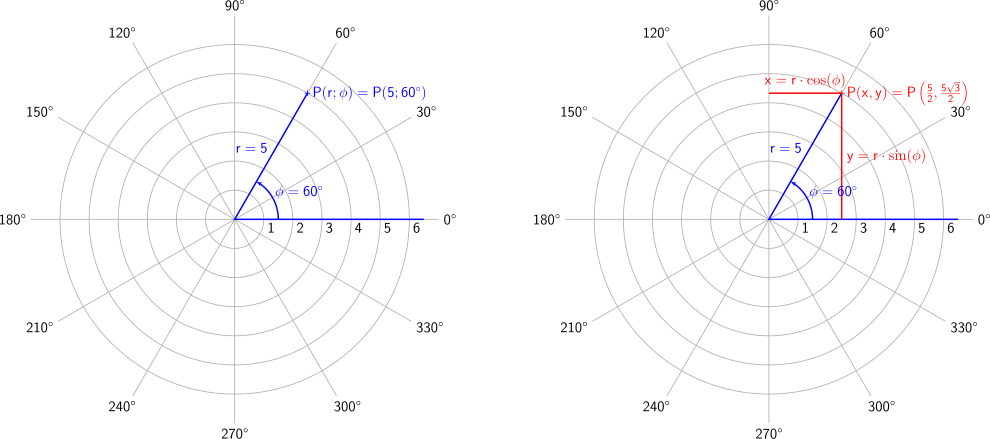
Eine völlig andere Variante eines Koordinatensystems sind die sogenannten Polarkoordinaten. Dieses System ist Vorteilhaft, wenn erstens eine Raumdimension vernachlässigbar ist und das Problem "Kreisförmiger Natur" ist.
Dieses Koordinatensystem besitzt anstelle der bekannten \(x\)- und \(y\)-Koordinaten eine Koordinante für den Winkel \(\varphi \) und eine Abstandskoordinante \(r\). Die Umrechnung erfolgt mit folgender Gleichung:
$$ \left(\begin{array}{c} x \\ y \end{array}\right) = \left(\begin{array}{c} r \cdot cos \varphi \\ r \cdot sin \varphi \end{array}\right) . \qquad (1.10)$$
oder umgekehrt:
$$ r= \sqrt{x^2+y^2}$$ $$ cos(\varphi) = \frac{x}{r} ; \qquad sin(\varphi) = \frac{y}{r} ; \qquad tan(\varphi) = \frac{y}{x}.$$
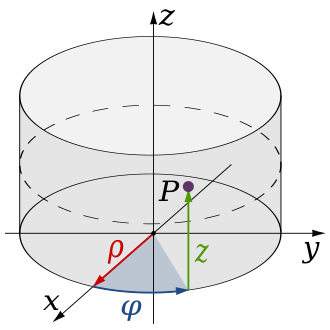
I.1.3.3 Zylinderkoordinaten:
Eine andere Variante ist die wenn das Problem von einer Sicht als Kreis betrachtet werden kann, jedoch eine gewisse höhe besitzt. Im Falle, dass die Kreisfläche mit der Höhe nicht varriert sondern konstant gleich groß bleibt, können Zylinderkoordinaten verwendet werden. Im Folgenden
BERECHNUNG FALSCH:
$$ r= \sqrt{x^2+y^2}$$ $$ cos(\varphi) = \frac{x}{r} ; \qquad sin(\varphi) = \frac{y}{r} ; \qquad tan(\varphi) = \frac{y}{x}.$$
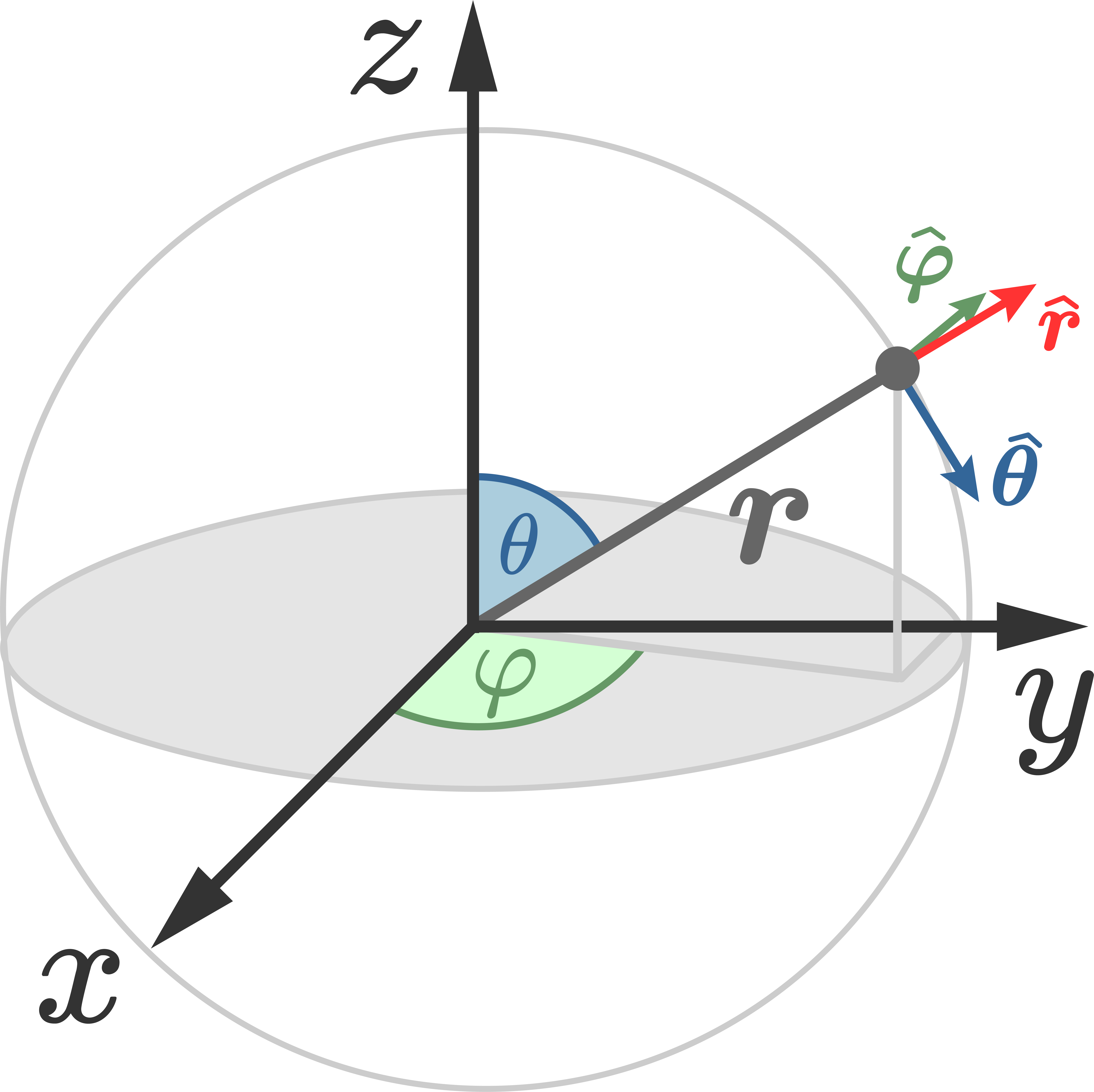
I.1.3.4 Kugelkoordinaten:
Die dritte Variante ein Koordinatensystem darzustellen ist mittels Kugelkoordinanten. Hierbei wird sich vorgestellt, dass eine aufgespannte Kugel um das Problem befindet. Mit einem Winkel \(\varphi \) und \(\vartheta \) kann die Position auf der Kugel bestimmt werden. Mit \(r \) kann zudem die Entfernung bis zu dem Punkt bestimmt werden. Visuell kann sich der Sternenhimmel vorgestellt werden, wenn eine Winkel horizontal zur Ebene und eine vertikal zur Ebene gegeben ist, können wir den Ort eines Sterns, Planeten oder anderen Himmelsobjekt bestimmen. Wollen wir zusätzlich die Entfernung zu dem Körper angeben müssen wir für \(r \) die Entfernung einsetzen.
BERECHNUNG FALSCH:
$$ r= \sqrt{x^2+y^2}$$ $$ cos(\varphi) = \frac{x}{r} ; \qquad sin(\varphi) = \frac{y}{r} ; \qquad tan(\varphi) = \frac{y}{x}.$$
I.1.4 Vielteilchensysteme
Die meisten Systeme in der Natur bestehen aus vielen Punktmassen. Ein Beispiel ist ein Kugelsternhaufen, welches aus tausenden Sternen und Planeten besteht, welche sich gegenseitig durch ihre Schwerkraft beeinflussen und somit chaotische Bewegungen im System durchführen. Aber auch ein Kubikmeter eines Gases wie unsere Luft besteht aus einer extrem hohen Anzahl Teilchen. Da die Lösugnen für die Bewegungsgleichung so hoher Anzahl von Teilchen jede Computerleistung übersteigen würde, können sich die Punktmassen als ein System vorgestellt werden.
I.1.4.1 Schwerpunkt eines Systems:
Bei einer hohen Anzahl \(N \) von Punktmassen \(m_i \) an den Orten \(\vec{x}_i \) werden Kräfte \(\vec{F}_i \) auf jeder dieser Punktmassen ausgeübt. Dabei kann können die wirkenden Kräfte aus unterschiedlichen Gründen entstehen. Einerseits führen die Punktmassen untereinander zu einer Kraft. Diese Inneren Kräfte z.B. von Masse \(m_a \) zu \(m_b \) bezeichnen wir als \(\vec{F}_{ab} \). Eine andere Kraft die auf eine Punktmasse wirken könnte, wäre eine Ursache die sich außerhalb des Systems befindet und wir als \(\vec{F}^{ext}_a \). Ein System ohne äußere Kräfte wird dann als isoliert bezeichnet. Die Gesamtkraft auf ein Teilchen \(a\) ist somit die Summe der äußeren und der inneren Kraft: $$ \vec{F}_{ges,a} = \vec{F}_{ab} + \vec{F}^{ext}_a $$ Für das Teilchen \(b\) ergibt sich analog: $$ \vec{F}_{ges,b} = \vec{F}_{ba} + \vec{F}^{ext}_b $$ Mittels des 3. Newtonschen Axiom ist bereits zu erkennen, dass im gemeinsamen System die Kräfte \(\vec{F}_{ab} \) + \(\vec{F}_{ba} \) = 0 ergeben und somit das die Bewegung des gesamt Systems nur durch die Äußere Kraft \(\vec{F}^{ext} \) beschreiben lassen. Um diese Bewegung zu beschreiben können die Punktmassen \(m_i \) zu einer Gesamtmasse \(M \) zusammengefasst werden: $$ M = \sum_i m_i, $$ der Schwerpunkt \(X \) ist dann: $$ \vec{X} = \frac{1}{M} \cdot \sum_i m_i \vec{x}_i. $$ Dieser Schwerpunkt kann sich als eine Punktmasse vorgestellt werden in der die Gesamtmasse vereinigt ist, auf die folgende Bewegungsgleichung wirkt: $$ \sum \vec{F}^{ext}_i = M\vec{X}. $$ Um anschliend die Informationen einer Punktmasse zu erhalten kann eine einfache Rücktransformation erfolgen.